TREE IN DATA STRUCTURE
In computer
science, a tree is a hierarchical data structure that consists of nodes
connected by edges.
It is used to
represent hierarchical relationships and is widely employed for organizing and
managing data efficiently.
A tree structure
is called a "tree" because it resembles an inverted tree, with the
root at the top and the branches (edges) leading downward to the leaves.
Trees are used in various applications, such as representing hierarchical structures (file systems, organizational charts), organizing data for efficient search and retrieval, and implementing various algorithms (e.g., binary search trees, AVL trees).
Fundamental terms:
1. Node:
- Definition: A fundamental building block
of a tree, containing data and pointers/references to its children (if any).
- Characteristics: Each node may have a
value or data, and it may have zero or more child nodes.
2. Root:
- Definition: The topmost node in a tree,
serving as the starting point for traversal.
- Characteristics: There is exactly one root
in a tree, and it has no parent.
3. Parent:
- Definition: A node in a tree that has one
or more child nodes.
- Characteristics: Each node, except the
root, has exactly one parent.
4. Child:
- Definition: Nodes directly connected to
another node when moving away from the root.
- Characteristics: A node may have zero or
more children.
5. Leaf:
- Definition: A node in a tree that has no
children, i.e., it is at the end of a branch.
- Characteristics: Leaf nodes are also
called terminal nodes.
6. Siblings:
- Definition: Nodes that share the same
parent.
- Characteristics: Nodes with the same
parent are considered siblings.
7. Ancestor:
- Definition: A node that lies on the path
between the root and another node.
- Characteristics: All nodes on the path
from the root to a particular node are ancestors of that node.
8. Descendant:
- Definition: A node in the subtree rooted
at another node.
- Characteristics: All nodes in the subtree
of a particular node are its descendants.
9. Subtree:
- Definition: A tree formed by a node and
all its descendants.
- Characteristics: Every node in a tree is
the root of its own subtree.
10. Depth:
- Definition: The level or distance of a
node from the root.
- Characteristics: The depth of the root is
0, and the depth increases as you move away from the root.
11. Height:
- Definition: The length of the longest
path from a node to a leaf.
- Characteristics: The height of a tree is
the height of the root. Leaf nodes have a height of 0.
Characteristics of
a tree:
1. Hierarchical
Structure:
- Definition: Nodes in a tree are organized
in a hierarchical or layered structure.
- Significance: This allows for the
representation of hierarchical relationships, making it suitable for modeling
structures like file systems or organizational charts.
2. One-to-Many
Relationships:
- Definition: A parent node can have
multiple child nodes, but each child node has only one parent.
- Significance: Enables the representation
of relationships where one entity has multiple sub-entities.
3. Directional
Relationships:
- Definition: The edges in a tree have a
direction, typically from parent to child.
- Significance: Defines a clear flow of
relationships, making it useful in representing processes or flowcharts.
4. Acyclic Nature:
- Definition: Trees are acyclic, meaning
there are no cycles or loops in the structure.
- Significance: Guarantees that you cannot
traverse a sequence of nodes and return to the starting node, ensuring
efficient traversal and preventing infinite loops.
5. Root Node:
- Definition: The topmost node in a tree is
called the root.
- Significance: Serves as the starting point
for any traversal operation, and it is the only node without a parent.
6. Leaf Nodes:
- Definition: Nodes with no children (at the
bottom of the tree) are called leaves.
- Significance: Represents endpoints in the
hierarchy, often containing specific data or information.
7. Siblings:
- Definition: Nodes that share the same
parent are called siblings.
- Significance: Provides a way to organize
and group related information or entities.
8. Depth:
- Definition: The level or distance of a
node from the root.
- Significance: Helps measure the depth of a
particular node within the hierarchy.
9. Height:
- Definition: The length of the longest path
from a node to a leaf.
- Significance: Measures the overall height
of the tree, indicating its overall size.
10. Balanced
Trees:
- Definition: Some tree structures, like
AVL trees or Red-Black trees, maintain balance.
- Significance: Ensures efficient
operations by preventing the tree from becoming highly skewed or unbalanced.
A simple visual
representation:
Root
/
\
Node1 Node2
/ \
Node3 Node4
In this example,
"Root" is the root node, "Node1" and "Node2" are
its children, and "Node3" and "Node4" are children of
"Node1." The structure continues to expand based on the relationships
between nodes.
--------------------------------------------------------------------
Advantages of
Trees:
1. Efficient Data
Retrieval:
- Trees provide efficient search, insertion,
and deletion operations, especially in balanced trees like AVL or Red-Black
trees.
- Searching for a particular element has a
time complexity of O(log n) in balanced trees.
2. Hierarchical
Representation:
- Trees naturally represent hierarchical
relationships, making them suitable for modeling hierarchical structures like
file systems, organizational charts, and family trees.
3. Sorting and
Range Queries:
- Binary Search Trees (BSTs) facilitate
sorting and range queries efficiently, as elements in the tree are ordered.
4. Balanced Trees
for Optimal Performance:
- Balanced trees, such as AVL or Red-Black
trees, maintain balance during insertions and deletions, ensuring optimal
performance for search operations.
5. Efficient for
Prefix Searches:
- Trie structures are trees commonly used
for efficient prefix searches, making them suitable for applications like
autocomplete functionality.
6. Natural
Representation of Expressions:
- Trees are used to represent mathematical
expressions in a way that reflects the hierarchical structure of the
expressions.
Disadvantages of Trees:
1. Complexity of
Implementation:
- Some tree structures, especially balanced
trees, can be complex to implement compared to simpler data structures like
arrays or linked lists.
2. Memory
Overhead:
- Trees may consume more memory than simpler
data structures due to the storage of pointers or references.
3. Unbalanced
Trees:
- In the absence of balancing mechanisms,
trees can become unbalanced, leading to performance degradation in terms of
search and retrieval.
Applications of Trees:
1. File Systems:
- Trees are used to represent file systems,
with directories as internal nodes and files as leaf nodes.
2. Database
Indexing:
- B-trees and other tree structures are
employed for indexing in databases, facilitating efficient search operations.
3. Organization
Charts:
- Trees can represent organizational
structures, with departments or positions as nodes and employees as leaf nodes.
4. Mathematical
Expression Evaluation:
- Trees are used to represent and evaluate
mathematical expressions, facilitating efficient expression parsing and
calculation.
5. Network Routing
Algorithms:
- Trees are employed in network routing
algorithms, where each node represents a network device, and the hierarchy
represents the structure of the network.
6. Game Trees in
AI:
- Trees are used to model game trees in
artificial intelligence, enabling decision-making processes in games.
7. HTML DOM
Structure:
- The Document Object Model (DOM) in web
development is represented as a tree structure, reflecting the hierarchical
organization of HTML elements.
Understanding the
advantages, disadvantages, and applications of trees helps in choosing the
appropriate data structure for specific use cases.
-----------------------------------------------------------------
Classification of
tree in data structure
Trees in data
structures can be classified based on various attributes such as branching
factors, balance, and specific properties. Here are some common classifications
of trees:
1. Based on Branching Factor:
# a. Binary Trees:
- Each node has at most two children: a left
child and a right child.
- Common types include Binary Search Trees
(BST), AVL Trees, and Red-Black Trees.
# b. Ternary
Trees:
- Each node has at most three children.
- Extensions include quaternary trees,
quinary trees, etc.
# c. k-ary Trees:
- Each node has at most k children.
- A binary tree is a special case where k =
2.
2. Based on Balance:
# a. Balanced
Trees:
- Maintain balance to ensure efficient
operations.
- Examples include AVL Trees and Red-Black
Trees.
# b. Unbalanced
Trees:
- The height of the tree can be
significantly skewed, leading to inefficient operations.
- Examples include skewed binary trees.
3. Based on Structure:
# a. Full Binary
Trees:
- Every node has either 0 or 2 children.
- The number of nodes at each level is a
power of 2.
# b. Complete
Binary Trees:
- All levels are completely filled, except
possibly the last level, which is filled from left to right.
# c. Perfect
Binary Trees:
- All internal nodes have exactly two
children.
- All leaf nodes are at the same level.
# d. Degenerate
(or pathological) Trees:
- Every parent node has only one associated
child node.
- Essentially a linked list.
4. Based on Representation:
# a. Binary Tree:
- Standard tree structure with at most two
children per node.
# b. Multiway
Tree:
- Nodes can have more than two children.
- Examples include Tries and B-trees.
5. Based on Specific Properties:
# a. Binary Search
Trees (BST):
- A binary tree where the left subtree of a
node contains only nodes with values less than the node, and the right subtree
contains only nodes with values greater than the node.
# b. Trie (Prefix
Tree):
- An ordered tree data structure used to
store a dynamic set or associative array.
# c. Huffman Tree:
- Used for compression algorithms, where
frequent symbols have shorter codes.
6. Based on Usage:
# a. Expression
Trees:
- Used to represent expressions in a tree
form, where operators are internal nodes, and operands are leaf nodes.
# b. Decision
Trees:
- Used in decision analysis and machine
learning for decision-making processes.
These
classifications provide a framework for understanding the diverse types and
applications of trees in computer science and data structures. Each type of
tree has specific advantages and use cases based on its properties and
characteristics.
--------------------------
BINARY TREE
·
A
binary tree is a hierarchical data structure composed of nodes, where each node
has at most two children, referred to as the left child and the right child.
·
Binary
trees are used in computer science for various purposes, such as organizing
data for efficient searching, sorting, and representing hierarchical
relationships.
·
Used
in various algorithms and data structures, such as binary search trees (BSTs),
binary heaps, expression trees, and more.
Figure from the web resource
Basic Terminology of Binary Trees:
1. Node:
- Each element in a binary tree is called a
node.
- A node contains data and may have a left
child and a right child.
2. Root:
- The topmost node in a binary tree is
called the root.
- It serves as the starting point for any
traversal.
3. Parent:
- A node in a binary tree that has one or
more children.
- The node above in the hierarchy is called
the parent.
4. Child:
- Nodes directly connected to another node
when moving away from the root.
- A node can have at most two children, a
left child and a right child.
5. Leaf (or
External Node):
- A node in a binary tree that has no
children is called a leaf.
- It is a node at the end of a branch.
6. Internal Node:
- A node with at least one child is called
an internal node.
- Internal nodes serve as branching points
in the tree.
7. Siblings:
- Nodes with the same parent are called
siblings.
- If a node has both a left and a right
child, they are siblings.
8. Subtree:
- A subtree is a tree formed by a node and
all its descendants.
9. Depth:
- The level or distance of a node from the
root.
- The depth of the root is 0.
10. Height (or
Depth of Tree):
- The length of the longest path from a
node to a leaf.
- The height of a tree is the height of the
root.
Features of Binary
Trees:
1. Binary
Structure:
- Each node in a binary tree has at most two
children, distinguishing it from other tree structures.
2. Hierarchical
Organization:
- Binary trees naturally represent
hierarchical relationships.
3. Efficient for
Search Operations:
- Binary search trees (BSTs), a type of
binary tree, allow for efficient search, insertion, and deletion operations
with a time complexity of O(log n) in average cases.
4. Versatility:
- Binary trees are used in a variety of
applications, including expression trees, Huffman coding, and hierarchical data
storage.
5. Traversal:
- Binary trees support different traversal
methods, including in-order, pre-order, and post-order traversal, each
providing a different sequence of visiting nodes.
6. Balanced and
Unbalanced Trees:
- Depending on the balance, binary trees can
be classified as balanced (e.g., AVL trees) or unbalanced, impacting the
efficiency of operations.
Binary trees are
foundational in computer science and provide a basis for more complex tree
structures and algorithms. They are widely used due to their simplicity and
efficiency in various applications.
Structure of a
Binary Tree:
·
A
binary tree is a hierarchical data structure composed of nodes, where each node
has at most two children, referred to as the left child and the right child.
·
The
topmost node is called the root, and nodes with no children are called leaves.
·
The
structure is recursive, as each subtree is itself a binary tree.
Binary Tree
Creation Algorithm:
1. Define a Node
structure to represent the nodes in the tree.
2. Create a
function to insert nodes into the tree.
3. Implement the
tree creation logic.
Example in C++: cpp
#include
<iostream>
using namespace
std;
// Node structure
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
// Function to
insert a node into the tree
TreeNode*
insert(TreeNode* root, int data) {
if (root == nullptr) {
return new TreeNode(data);
}
if (data < root->data) {
root->left = insert(root->left,
data);
} else {
root->right = insert(root->right,
data);
}
return root;
}
// Example usage
int main() {
TreeNode* root = nullptr;
// Inserting nodes into the tree
root = insert(root, 5);
root = insert(root, 3);
root = insert(root, 7);
root = insert(root, 2);
root = insert(root, 4);
// Additional operations can be performed
here
return 0;
}
Example in Python: python
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function to
insert a node into the tree
def insert(root,
data):
if root is None:
return TreeNode(data)
if data < root.data:
root.left = insert(root.left, data)
else:
root.right = insert(root.right, data)
return root
# Example usage
root = None
# Inserting nodes
into the tree
root =
insert(root, 5)
root =
insert(root, 3)
root =
insert(root, 7)
root =
insert(root, 2)
root =
insert(root, 4)
The resulting tree
will have the properties of a binary search tree, where nodes to the left are
smaller, and nodes to the right are larger than the current node.
Classification of
Binary Trees:
Binary trees can
be classified based on various criteria, including structure, shape, and
properties. Here are some common classifications:
1. Based on Shape/Structure:
# a. Full Binary
Tree:
- Every node has either 0 or 2 children.
- All leaf nodes are at the same level.
# b. Complete
Binary Tree:
- All levels are completely filled, except
possibly the last level.
- Nodes are added from left to right.
# c. Perfect
Binary Tree:
- All internal nodes have exactly two
children.
- All leaf nodes are at the same level.
# d. Skewed or
Degenerate Tree:
- Each node has only one child.
- Essentially a linked list.
2. Based on Height/Balance:
# a. Balanced
Binary Tree:
- The height of the left and right subtrees
of any node differs by at most one.
- Examples include AVL trees and Red-Black
trees.
# b. Unbalanced
Binary Tree:
- The height of the subtrees can differ
significantly.
- May lead to performance issues in terms of
search and retrieval.
3. Based on Traversal Order:
# a. Strict/Proper
Binary Tree:
- Every node has either 0 or 2 children.
- No node has only one child.
# b. Complete
Binary Search Tree (CBST):
- A binary search tree that is also
complete.
4. Based on Node Relationships:
# a. Binary Search
Tree (BST):
- The left subtree of a node contains only
nodes with values less than the node.
- The right subtree contains only nodes with
values greater than the node.
# b. Heap:
- A complete binary tree that satisfies the
heap property.
- Max heap: Each node is greater than or
equal to its children.
- Min heap: Each node is less than or equal
to its children.
5. Based on Special Properties:
# a. Expression
Tree:
- Used to represent mathematical
expressions.
- Internal nodes represent operators, and
leaves represent operands.
# b. Huffman Tree:
- Used in compression algorithms.
- Represents characters in a way that
minimizes the total number of bits required.
These
classifications help in understanding the different types and characteristics
of binary trees, each suited to particular use cases and applications.
example implementation in C++ and Python:
Binary Search Tree (BST) Creation Algorithm:
Fig. from the web resource
1. Define a Node
structure to represent nodes in the tree.
2. Create a
function to insert nodes into the BST.
3. Implement the
logic to maintain the BST property.
Example in C++: cpp
#include
<iostream>
using namespace
std;
// Node structure
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
// Function to
insert a node into the BST
TreeNode*
insert(TreeNode* root, int data) {
if (root == nullptr) {
return new TreeNode(data);
}
if (data < root->data) {
root->left = insert(root->left,
data);
} else {
root->right = insert(root->right,
data);
}
return root;
}
// Example usage
int main() {
TreeNode* root = nullptr;
// Inserting nodes into the BST
root = insert(root, 5);
root = insert(root, 3);
root = insert(root, 7);
root = insert(root, 2);
root = insert(root, 4);
// Additional operations can be performed
here
return 0;
}
---------------
Example in Python: python
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function to
insert a node into the BST
def insert(root,
data):
if root is None:
return TreeNode(data)
if data < root.data:
root.left = insert(root.left, data)
else:
root.right = insert(root.right, data)
return root
# Example usage
root = None
# Inserting nodes
into the BST
root =
insert(root, 5)
root =
insert(root, 3)
root = insert(root,
7)
root =
insert(root, 2)
root =
insert(root, 4)
------------------------------
Advantages of Binary Trees:
1. Efficient
Search Operations:
- Binary Search Trees (BSTs) provide
efficient search, insertion, and deletion operations with an average time
complexity of O(log n).
2. Simple
Structure:
- Binary trees have a simple and intuitive
structure, making them easy to implement and understand.
3. Memory
Efficiency:
- Binary trees can be memory-efficient,
especially when compared to more complex data structures like hash tables.
4. Sorting:
- BSTs naturally maintain the order of
elements, making them suitable for scenarios where data needs to be sorted.
5. Efficient Range
Queries:
- BSTs allow for efficient range queries,
where a range of values needs to be retrieved from the tree.
6. Versatility:
- Binary trees serve as the foundation for
more advanced tree structures and algorithms, making them versatile in computer
science.
---------------------------------
Disadvantages of
Binary Trees:
1. Unbalanced
Trees:
- In the absence of balancing mechanisms,
binary trees can become unbalanced, leading to skewed structures and degraded
performance.
2. Performance
Degradation in Worst Case:
- In the worst case, if the tree is highly
unbalanced, the time complexity of operations may degrade to O(n), where n is
the number of nodes.
3. Complex
Balancing Mechanisms:
- Implementing and maintaining balanced
binary trees (e.g., AVL or Red-Black trees) can be complex, requiring careful
handling of rotations and adjustments.
4. Limited Sorting
Order:
- Binary trees only maintain order based on
the key values, which might limit sorting options for certain scenarios.
---------------------------------------
Applications of Binary Trees:
1. Symbol Tables:
- Binary search trees are commonly used in
symbol tables to efficiently store and retrieve key-value pairs.
2. File Systems:
- Binary trees are used in file systems to
represent hierarchical directory structures.
3. Expression
Trees:
- Binary trees represent mathematical
expressions, where operators are internal nodes, and operands are leaf nodes.
4. Network Routing
Algorithms:
- Binary trees are applied in network
routing algorithms, representing the hierarchical structure of network nodes.
5. Database
Indexing:
- Binary trees, such as B-trees, are used
for indexing in databases, facilitating efficient search operations.
6. Game Trees in
AI:
- Binary trees model decision trees in
game-playing algorithms for artificial intelligence.
7. Huffman Coding:
- Huffman trees, a type of binary tree, are
used for data compression, assigning shorter codes to more frequent symbols.
8. Expression
Parsing:
- Binary trees are utilized in parsing and
evaluating mathematical expressions.
---------------------------------------------------------------------------------------------------------------
Algorithm of
Representation as Array and link List,
In a binary tree,
there are two common ways to represent it: using an array (linear
representation) or using a linked structure. Below are the algorithms for both
representations.
Binary Tree Representation as an Array:
Fig. from
web resource
1. Algorithm for
Insertion:
Fig. from the web resource
Algorithm insertArray(tree, value):
Input: Binary tree represented as an array,
value to be inserted
Output: Updated binary tree array
1. Find the first available position in the
array, typically starting from index 1.
2. Insert the value at the found position.
2. Algorithm for
Accessing Nodes:
Algorithm
accessArray(tree, index):
Input: Binary tree represented as an array,
index of the node
Output: Value of the node at the given
index
1. Return the value stored at the specified
index in the array.
3. Algorithm for
Traversal (e.g., In-order Traversal):
Algorithm
inOrderTraversalArray(tree, index):
Input: Binary tree represented as an array,
index of the root node
Output: Traversal of the binary tree in an in-order fashion
1. If the left child of the node at the
given index exists, recursively call inOrderTraversalArray with the left
child's index.
2. Process the node at the given index
(e.g., print its value).
3. If the right child of the node at the
given index exists, recursively call inOrderTraversalArray with the right
child's index.
---------------------------------------------
Binary Tree Representation as a Linked List:
Fig. from the web resource
1. Algorithm for
Node Definition:
Algorithm
Node(value):
Input: Value to be stored in the node
Output: New node with the given value
1. Create a new node.
2. Set the value of the node to the given
value.
3. Set the left and right child pointers to
null.
4. Return the new node.
2. Algorithm for
Insertion:
Algorithm
insertLinkedList(root, value):
Input: Root of the binary tree represented
as a linked list, value to be inserted
Output: Updated binary tree linked list
1. If the root is null, create a new node
with the given value and set it as the root.
2. If the value is less than the root's
value, recursively call insertLinkedList with the left child of the root and
the given value.
3. If the value is greater than or equal to
the root's value, recursively call insertLinkedList with the right child of the
root and the given value.
4. Return the root of the modified binary
tree.
3. Algorithm for
Traversal (e.g., In-order Traversal):
Algorithm
inOrderTraversalLinkedList(root):
Input: Root of the binary tree represented
as a linked list
Output: Traversal of the binary tree in an in-order fashion
1. If the root is not null:
a. Recursively call
inOrderTraversalLinkedList with the left child of the root.
b. Process the root node (e.g., print
its value).
c. Recursively call
inOrderTraversalLinkedList with the right child of the root.
Representation as an Array:
# C++ Example: cpp
#include
<iostream>
#include
<vector>
using namespace
std;
// Representation
of Binary Tree using Array
class
BinaryTreeArray {
private:
vector<int> treeArray;
public:
// Constructor
BinaryTreeArray() {}
// Insertion Algorithm
void insertArray(int value) {
treeArray.push_back(value);
}
// Accessing Nodes Algorithm
int accessArray(int index) {
if (index >= 0 && index <
treeArray.size()) {
return treeArray[index];
} else {
cerr << "Index out of
bounds!" << endl;
return -1; // Return a default value or handle the error
accordingly
}
}
// In-order Traversal Algorithm
void inOrderTraversalArray(int index) {
if (index < treeArray.size()) {
inOrderTraversalArray(2 * index +
1); // Left child
cout << treeArray[index]
<< " ";
inOrderTraversalArray(2 * index +
2); // Right child
}
}
};
// Example Usage
int main() {
BinaryTreeArray tree;
// Inserting nodes into the array
tree.insertArray(5);
tree.insertArray(3);
tree.insertArray(7);
tree.insertArray(2);
tree.insertArray(4);
// Accessing nodes and in-order traversal
cout << "Node at index 2: "
<< tree.accessArray(2) << endl;
cout << "In-order Traversal:
";
tree.inOrderTraversalArray(0);
cout << endl;
return 0;
}
-------------------------------------
# Python Example: python
# Representation
of Binary Tree using Array
class
BinaryTreeArray:
def __init__(self):
self.tree_array = []
# Insertion Algorithm
def insert_array(self, value):
self.tree_array.append(value)
# Accessing Nodes Algorithm
def access_array(self, index):
if 0 <= index <
len(self.tree_array):
return self.tree_array[index]
else:
print("Index out of
bounds!")
return -1 # Return a default value or handle the error
accordingly
# In-order Traversal Algorithm
def in_order_traversal_array(self, index):
if index < len(self.tree_array):
self.in_order_traversal_array(2 *
index + 1) # Left child
print(self.tree_array[index],
end=" ")
self.in_order_traversal_array(2 *
index + 2) # Right child
# Example Usage
tree =
BinaryTreeArray()
# Inserting nodes
into the array
tree.insert_array(5)
tree.insert_array(3)
tree.insert_array(7)
tree.insert_array(2)
tree.insert_array(4)
# Accessing nodes
and in-order traversal
print("Node
at index 2:", tree.access_array(2))
print("In-order
Traversal:", end=" ")
tree.in_order_traversal_array(0)
print()
-----------------------------------------
Representation as a Linked List:
# C++ Example: cpp
#include
<iostream>
using namespace
std;
// Node Definition
for Linked List Representation
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
// Representation
of Binary Tree using Linked List
class
BinaryTreeLinkedList {
private:
TreeNode* root;
public:
// Constructor
BinaryTreeLinkedList() : root(nullptr) {}
// Insertion Algorithm
TreeNode* insert_linked_list(TreeNode*
node, int value) {
if (node == nullptr) {
return new TreeNode(value);
}
if (value < node->data) {
node->left =
insert_linked_list(node->left, value);
} else {
node->right =
insert_linked_list(node->right, value);
}
return node;
}
// In-order Traversal Algorithm
void
in_order_traversal_linked_list(TreeNode* node) {
if (node != nullptr) {
in_order_traversal_linked_list(node->left); // Left child
cout << node->data
<< " ";
in_order_traversal_linked_list(node->right); // Right child
}
}
};
// Example Usage
int main() {
BinaryTreeLinkedList tree;
// Inserting nodes into the linked list
tree.insert_linked_list(tree.root, 5);
tree.insert_linked_list(tree.root, 3);
tree.insert_linked_list(tree.root, 7);
tree.insert_linked_list(tree.root, 2);
tree.insert_linked_list(tree.root, 4);
// In-order traversal
cout << "In-order Traversal:
";
tree.in_order_traversal_linked_list(tree.root);
cout << endl;
return 0;
}
-------------------------------------------
# Python Example:
python
# Node Definition
for Linked List Representation
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
# Representation
of Binary Tree using Linked List
class BinaryTreeLinkedList:
def __init__(self):
self.root = None
# Insertion Algorithm
def insert_linked_list(self, node, value):
if node is None:
return TreeNode(value)
if value < node.data:
node.left =
self.insert_linked_list(node.left, value)
else:
node.right =
self.insert_linked_list(node.right, value)
return node
# In-order Traversal Algorithm
def in_order_traversal_linked_list(self,
node):
if node is not None:
self.in_order_traversal_linked_list(node.left) # Left child
print(node.data, end=" ")
self.in_order_traversal_linked_list(node.right) # Right child
# Example Usage
tree =
BinaryTreeLinkedList()
# Inserting nodes
into the linked list
tree.root =
tree.insert_linked_list(tree.root, 5)
tree.root =
tree.insert_linked_list(tree.root, 3)
tree.root =
tree.insert_linked_list(tree.root, 7)
tree.root = tree.insert_linked_list(tree.root,
2)
tree.root =
tree.insert_linked_list(tree.root, 4)
# In-order
traversal
print("In-order
Traversal:", end=" ")
tree.in_order_traversal_linked_list(tree.root)
print()
----------------------------
In this Python example, the `TreeNode` class represents a node in the linked list representation of the binary tree. The `BinaryTreeLinkedList` class includes methods for insertion (`insert_linked_list`) and in-order traversal (`in_order_traversal_linked_list`). The example demonstrates the creation of the binary tree and performs an in-order traversal. Basic operation of Binary tree in data structure
------------------------------------------------------------------------------------------------------------
Algorithms of
operation of Binary tree
Binary Tree Operations:
# 1. Insertion
Operation:
Algorithm:
Algorithm
insertBinaryTree(root, value):
Input: Root of the binary tree, value to be
inserted
Output: Updated binary tree
1. If the root is null, create a new node
with the given value and set it as the root.
2. If the value is less than the root's
value, recursively call insertBinaryTree with the left child of the root and
the given value.
3. If the value is greater than or equal to
the root's value, recursively call insertBinaryTree with the right child of the
root and the given value.
4. Return the root of the modified binary
tree.
C++ Example: cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
TreeNode*
insertBinaryTree(TreeNode* root, int value) {
if (root == nullptr) {
return new TreeNode(value);
}
if (value < root->data) {
root->left =
insertBinaryTree(root->left, value);
} else {
root->right =
insertBinaryTree(root->right, value);
}
return root;
}
// Example Usage
int main() {
TreeNode* root = nullptr;
root = insertBinaryTree(root, 5);
root = insertBinaryTree(root, 3);
root = insertBinaryTree(root, 7);
root = insertBinaryTree(root, 2);
root = insertBinaryTree(root, 4);
// Additional operations can be performed
here
return 0;
}
------------------------------
Python Example: python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def
insert_binary_tree(root, value):
if root is None:
return TreeNode(value)
if value < root.data:
root.left =
insert_binary_tree(root.left, value)
else:
root.right =
insert_binary_tree(root.right, value)
return root
# Example Usage
root = None
root =
insert_binary_tree(root, 5)
root =
insert_binary_tree(root, 3)
root =
insert_binary_tree(root, 7)
root =
insert_binary_tree(root, 2)
root =
insert_binary_tree(root, 4)
# Additional
operations can be performed here
# 2. Traversal
Operations: Algorithm
for In-order Traversal:
Algorithm
inOrderTraversal(root):
Input: Root of the binary tree
Output: In-order traversal of the binary
tree
1. If the root is not null:
a. Recursively call inOrderTraversal
with the left child of the root.
b. Process the root node (e.g., print
its value).
c. Recursively call inOrderTraversal
with the right child of the root.
C++ Example: cpp
void
inOrderTraversal(TreeNode* root) {
if (root != nullptr) {
inOrderTraversal(root->left);
cout << root->data <<
" ";
inOrderTraversal(root->right);
}
}
// Example Usage
// Assuming 'root'
is the root of the binary tree
inOrderTraversal(root);
Python Example: Python
def
in_order_traversal(root):
if root is not None:
in_order_traversal(root.left)
print(root.data, end=" ")
in_order_traversal(root.right)
# Example Usage
# Assuming 'root'
is the root of the binary tree
in_order_traversal(root)
# 3. Deletion
Operation (Node Removal):
Deletion in binary
trees can be more complex due to different cases (node with no children, node
with one child, node with two children). The example below shows a simplified
case where the node to be deleted has at most one child.
Algorithm:
Algorithm
deleteNode(root, value):
Input: Root of the binary tree, value to be
deleted
Output: Updated binary tree
1. If the root is null, return null.
2. If the value is less than the root's
value, recursively call deleteNode with the left child of the root.
3. If the value is greater than the root's
value, recursively call deleteNode with the right child of the root.
4. If the value is equal to the root's
value:
a. If the root has no left child,
return the right child.
b. If the root has no right child,
return the left child.
c. If the root has both left and right
children:
i. Find the smallest node in the
right subtree (or the largest node in the left subtree).
ii. Replace the root's value with
the value of the found node.
iii. Recursively call deleteNode to
remove the found node from the right (or left) subtree.
5. Return the root of the modified binary
tree.
C++ Example:cpp
TreeNode*
findMin(TreeNode* node) {
while (node->left != nullptr) {
node = node->left;
}
return node;
}
TreeNode*
deleteNode(TreeNode* root, int value) {
if (root == nullptr) {
return nullptr;
}
if (value < root->data) {
root->left =
deleteNode(root->left, value);
} else if (value > root->data) {
root->right =
deleteNode(root->right, value);
} else {
if (root->left == nullptr) {
TreeNode* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
TreeNode* temp = root->left;
delete root;
return temp;
}
TreeNode* temp =
findMin(root->right);
root->data = temp->data;
root->right =
deleteNode(root->right, temp->data);
}
return root;
}
// Example Usage
// Assuming 'root'
is the root of the binary tree
root =
deleteNode(root, 3);
----------------------------------
Python Example: python
def
find_min(node):
while node.left is not None:
node = node.left
return node
def
delete_node(root, value):
if root is None:
return None
if value < root.data:
root.left = delete_node(root.left,
value)
elif value > root.data:
root.right = delete_node(root.right,
value)
else:
if root.left is None:
temp = root.right
del root
return temp
elif root.right is None:
temp = root.left
del root
return temp
temp = find_min(root.right)
root.data = temp.data
root.right = delete_node(root.right,
temp.data)
return root
# Example Usage
# Assuming 'root'
is the root of the binary tree
root =
delete_node(root, 3)
These examples
cover the basic operations of inserting nodes, traversing the binary tree
(in order), and deleting nodes (with one or no children). Real-world scenarios
may require more complex deletion algorithms depending on the specific
requirements and constraints. Additionally, handling cases where nodes have two
children involves more intricate logic to maintain the properties of a binary
search tree.
------------------------------------------------
TRAVERSING TREE
Tree traversal is
the process of visiting and processing each node in a tree data structure.
There are three main techniques for traversing a tree: in-order traversal,
pre-order traversal, and post-order traversal. These techniques define the
order in which nodes are visited, and they have different applications based on
the specific requirements of the task at hand.
1. In-order Traversal:
In in-order
traversal, the left subtree is visited first, followed by the root node, and
then the right subtree. This results in nodes being visited in ascending order
in a binary search tree.
Algorithm:
Algorithm inOrderTraversal(node):
Input: Root of the tree or subtree
Output: In-order traversal of the tree or
subtree
1. If the node is not null:
a. Recursively call inOrderTraversal
with the left child of the node.
b. Process the node (e.g., print its
value).
c. Recursively call inOrderTraversal
with the right child of the node.
Example:-
A
/ \
B
C
/ \ / \
D E
F G
Traversal Path:
- Traverse left subtree: D -> E
- Visit root: A
- Traverse right subtree: B -> C -> F -> G
Therefore, the in-order traversal visits the nodes
in the following order: D E A B C F G.
Explanation:
- In-order traversal follows a Left-Root-Right pattern.
- First, it visits all nodes in the left subtree completely.
- Then, it visits the root node.
- Finally, it visits all nodes in the right subtree completely.
This diagram demonstrates the process for a simple binary tree.
2. Pre-order Traversal:
In pre-order
traversal, the root node is visited first, followed by the left subtree and
then the right subtree. This traversal is useful for creating a copy of the
tree or evaluating an expression tree.
Algorithm:
Algorithm
preOrderTraversal(node):
Input: Root of the tree or subtree
Output: Pre-order traversal of the tree or
subtree
1. If the node is not null:
a. Process the node (e.g., print its
value).
b. Recursively call preOrderTraversal
with the left child of the node.
c. Recursively call preOrderTraversal
with the right child of the node.
Example :
A / \ B C / \ / \ D E F GTraversal Path:
1. Visit root: A
2. Traverse left subtree: D -> E
3. Traverse right subtree: B -> C -> F -> G
Therefore, the pre-order traversal visits the nodes in the following
order: A
D E B C F G.
Explanation:
·
Pre-order traversal follows a Root-Left-Right pattern.
·
First, it visits the root node.
·
Then, it traverses the left subtree completely.
·
Finally, it traverses the right subtree completely.
This diagram demonstrates the process for the same binary tree used in the in-order traversal example.
3. Post-order Traversal:
In post-order
traversal, the left subtree is visited first, followed by the right subtree,
and then the root node. This traversal is often used in deleting nodes from a
tree or evaluating an expression tree.
Algorithm:
Algorithm
postOrderTraversal(node):
Input: Root of the tree or subtree
Output: Post-order traversal of the tree or
subtree
1. If the node is not null:
a. Recursively call postOrderTraversal
with the left child of the node.
b. Recursively call postOrderTraversal
with the right child of the node.
c. Process the node (e.g., print its
value).
example:
F
/ \
B
G
/ \
\
A
D I
/ \
\
C
E H
The post-order traversal of this binary tree
would be: A, C, E, D, B, H, I, G, F.
In post-order traversal, we first visit the
left subtree, then the right subtree, and finally the root node. Here’s how it
works for the above tree:
- Start from the root (F).
- Traverse the left subtree in post-order (B).
- Visit B’s left subtree (A). Since A is a leaf node, we add it to our traversal.
- Visit B’s right subtree (D).
- Visit D’s left subtree (C). Since C is a leaf node, we add it to our traversal.
- Visit D’s right subtree (E). Since E is a leaf node, we add it to our traversal.
- Visit D. Add D to our traversal.
- Visit B. Add B to our traversal.
- Traverse the right subtree in post-order (G).
- Visit G’s right subtree (I).
- Visit I’s right subtree (H). Since H is a leaf node, we add it to our traversal.
- Visit I. Add I to our traversal.
- Visit G. Add G to our traversal.
- Visit the root (F). Add F to
our traversal.
So, the post-order traversal of this tree is A, C, E, D,
B, H, I, G, F. This means we first visit the leftmost node,
then its parent’s right node (if any), then the parent itself, and we repeat
this process for each subtree. After we finish with the left subtree, we do the
same for the right subtree. Finally, we visit the root node.
Example in C++: cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
void
inOrderTraversal(TreeNode* root) {
if (root != nullptr) {
inOrderTraversal(root->left);
cout << root->data <<
" ";
inOrderTraversal(root->right);
}
}
void
preOrderTraversal(TreeNode* root) {
if (root != nullptr) {
cout << root->data <<
" ";
preOrderTraversal(root->left);
preOrderTraversal(root->right);
}
}
void
postOrderTraversal(TreeNode* root) {
if (root != nullptr) {
postOrderTraversal(root->left);
postOrderTraversal(root->right);
cout << root->data <<
" ";
}
}
// Example Usage
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "In-order Traversal:
";
inOrderTraversal(root);
cout << endl;
cout << "Pre-order Traversal:
";
preOrderTraversal(root);
cout << endl;
cout << "Post-order Traversal:
";
postOrderTraversal(root);
cout << endl;
return 0;
}
------------------------------------------------
Example in Python: python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def
in_order_traversal(root):
if root is not None:
in_order_traversal(root.left)
print(root.data, end=" ")
in_order_traversal(root.right)
def
pre_order_traversal(root):
if root is not None:
print(root.data, end=" ")
pre_order_traversal(root.left)
pre_order_traversal(root.right)
def
post_order_traversal(root):
if root is not None:
post_order_traversal(root.left)
post_order_traversal(root.right)
print(root.data, end=" ")
# Example Usage
root = TreeNode(1)
root.left =
TreeNode(2)
root.right =
TreeNode(3)
root.left.left =
TreeNode(4)
root.left.right =
TreeNode(5)
print("In-order
Traversal:", end=" ")
in_order_traversal(root)
print()
print("Pre-order
Traversal:", end=" ")
pre_order_traversal(root)
print()
print("Post-order
Traversal:", end=" ")
post_order_traversal(root)
print()
These tree
traversal techniques are essential for various applications, such as searching,
printing, evaluating expressions, and more. The choice of traversal depends on
the specific task and the desired order of processing nodes in the tree.
--------------
IN ORDER TREE
TRAVERSING
In-order tree
traversal is a depth-first tree traversal algorithm that visits the nodes of a
binary tree in a specific order.
In this traversal,
each node is processed between its left and right subtrees.
The in-order
traversal is named after the order in which nodes are visited: left subtree,
current node, right subtree.
Features of In-order Tree Traversal:
1. Order of
Processing:
- The nodes are processed in the order: left
subtree, current node, right subtree.
2. Binary Search
Trees (BST):
- In-order traversal of a binary search tree
results in visiting nodes in ascending order (or non-decreasing order) of their
values.
3. Recursion:
- In-order traversal is naturally
implemented using recursion, where the function calls itself for the left and
right subtrees.
4. Depth-First
Traversal:
- In-order traversal is a depth-first
traversal method, exploring as far as possible along each branch before
backtracking.
5. Useful for
Expression Trees:
- In-order traversal is often used to
traverse expression trees, producing an infix expression.
Structure of In-order Tree Traversal:
Algorithm:
Algorithm
inOrderTraversal(node):
Input: Root of the tree or subtree
Output: In-order traversal of the tree or
subtree
1. If the node is not null:
a. Recursively call inOrderTraversal
with the left child of the node.
b. Process the node (e.g., print its
value).
c. Recursively call inOrderTraversal
with the right child of the node.
Pseudocode:
inOrderTraversal(node):
if node is not null:
inOrderTraversal(node.left)
process(node)
inOrderTraversal(node.right)
Example in C++: cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
void
inOrderTraversal(TreeNode* root) {
if (root != nullptr) {
inOrderTraversal(root->left);
cout << root->data <<
" ";
inOrderTraversal(root->right);
}
}
// Example Usage
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "In-order Traversal:
";
inOrderTraversal(root);
cout << endl;
return 0;
}
---------------------------------
Example in Python: python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def in_order_traversal(root):
if root is not None:
in_order_traversal(root.left)
print(root.data, end=" ")
in_order_traversal(root.right)
# Example Usage
root = TreeNode(1)
root.left =
TreeNode(2)
root.right =
TreeNode(3)
root.left.left =
TreeNode(4)
root.left.right =
TreeNode(5)
print("In-order
Traversal:", end=" ")
in_order_traversal(root)
print()
------------------------------------------------------
Advantages of In-order Tree Traversal:
1. Sorting:
- One of the primary advantages of in-order
tree traversal is that, for binary search trees (BST), it results in visiting
nodes in ascending order. This property makes in-order traversal an efficient
way to obtain a sorted sequence of elements from a BST.
2. Expression
Trees:
- In-order traversal is commonly used in
expression trees to generate the infix expression. The resulting expression
maintains the proper order of operations and is easily understandable.
3. BST Validation:
- In-order traversal can be used to validate
whether a binary tree is a binary search tree (BST). If the nodes are visited
in ascending order, it indicates that the tree adheres to the properties of a
BST.
4. Searching:
- In-order traversal is beneficial for
searching in a binary search tree. As the nodes are visited in sorted order, it
allows for efficient searching operations.
--------------------------------------------------
Disadvantages of In-order Tree Traversal:
1. Not Suitable
for All Operations:
- While in-order traversal is advantageous
for certain operations like sorting, it may not be the most efficient choice
for other tasks. For example, if the goal is to find the minimum or maximum
value in a BST, in-order traversal is not the most direct approach.
2. Not Suitable
for Balanced Trees:
- For perfectly balanced trees, in-order
traversal might not provide significant advantages over other traversal
methods. In such cases, the balance of the tree ensures that all nodes are
accessible efficiently through other traversal strategies.
-----------------------------------------------------
Application of In-order Tree Traversal:
1. Sorting:
- In-order traversal is widely used for
sorting elements stored in a binary search tree. The resulting sorted sequence
can be used for various applications where ordered data is required.
2. Expression
Evaluation:
- In-order traversal is employed in
expression trees for generating infix expressions. This is especially useful in
compiler design and parsing expressions.
3. Binary Search
Trees (BST):
- In-order traversal is a fundamental
operation in working with binary search trees. It helps in searching for
elements, validating the tree's structure, and obtaining elements in sorted
order.
4. Data Retrieval:
- In-order traversal is useful when the goal
is to retrieve data in a sorted manner. For example, retrieving a list of
contacts from an address book stored in a BST.
-------------------------------------------------
Pre-order Tree
Traversal:
Pre-order tree
traversal is a depth-first tree traversal algorithm that processes each node in
a binary tree in a specific order. In this traversal, the algorithm visits the
root node before its left and right subtrees.
The term
"pre-order" indicates that the root is processed before (pre) its
children.
Features of Pre-order Tree Traversal:
1. Order of
Processing:
- The nodes are processed in the order:
current node, left subtree, right subtree.
2. Depth-First
Traversal:
- Pre-order traversal is a depth-first
traversal method, exploring as far as possible along each branch before
backtracking.
3. Useful for
Copying Trees:
- It is useful for creating a copy of the
tree, as the current node is processed before its subtrees.
4. Expression
Trees:
- Pre-order traversal is often used in
expression trees to generate a prefix expression.
-------------------------------------------------------------
Structure of Pre-order Tree Traversal:
Algorithm:
Algorithm
preOrderTraversal(node):
Input: Root of the tree or subtree
Output: Pre-order traversal of the tree or
subtree
1. If the node is not null:
a. Process the node (e.g., print its
value).
b. Recursively call preOrderTraversal
with the left child of the node.
c. Recursively call preOrderTraversal
with the right child of the node.
Pseudocode:
preOrderTraversal(node):
if node is not null:
process(node)
preOrderTraversal(node.left)
preOrderTraversal(node.right)
Example in C++:cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
void
preOrderTraversal(TreeNode* root) {
if (root != nullptr) {
cout << root->data <<
" ";
preOrderTraversal(root->left);
preOrderTraversal(root->right);
}
}
// Example Usage
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "Pre-order Traversal:
";
preOrderTraversal(root);
cout << endl;
return 0;
}
-----------------------------------
Example in Python:python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def pre_order_traversal(root):
if root is not None:
print(root.data, end=" ")
pre_order_traversal(root.left)
pre_order_traversal(root.right)
# Example Usage
root = TreeNode(1)
root.left =
TreeNode(2)
root.right =
TreeNode(3)
root.left.left =
TreeNode(4)
root.left.right =
TreeNode(5)
print("Pre-order
Traversal:", end=" ")
pre_order_traversal(root)
print()
-----------------------------------------
Advantages of Pre-order Tree Traversal:
1. Expression
Evaluation:
- Useful for evaluating expressions
represented by expression trees, particularly for generating prefix
expressions.
2. Copying Trees:
- Suitable for creating a copy of a tree, as
it starts processing nodes from the root.
3. Depth-First
Search:
- Effective for depth-first searches when
the order of processing requires nodes to be visited before their descendants.
------------------------------------------------------
Disadvantages of
Pre-order Tree Traversal:
1. Not Suitable
for Sorting:
- Unlike in-order traversal, pre-order
traversal does not produce elements in sorted order, making it less suitable
for sorting tasks.
------------------------------------------
Application of
Pre-order Tree Traversal:
1. Expression
Evaluation:
- Used in expression trees to generate
prefix expressions, which can be directly evaluated.
2. Creating a Copy
of a Tree:
- Suitable for creating a copy of a tree,
where nodes are processed before their subtrees. This is helpful when
maintaining the original structure of the tree is necessary.
3. Depth-First
Searches:
- Effective for depth-first searches and
tree processing when the order requires nodes to be visited before their
descendants.
4. Binary Tree
Serialization:
- Pre-order traversal can be used for
serializing a binary tree, allowing for its efficient storage and later
reconstruction.
-----------------
Post-order Tree
Traversal:
Post-order tree
traversal is a depth-first tree traversal algorithm that processes each node in
a binary tree in a specific order.
In this traversal,
the algorithm visits the left and right subtrees before processing the root
node.
The term
"post-order" indicates that the children are processed before (post)
the current node.
Features of Post-order Tree Traversal:
1. Order of
Processing:
- The nodes are processed in the order: left
subtree, right subtree, current node.
2. Depth-First
Traversal:
- Post-order traversal is a depth-first
traversal method, exploring as far as possible along each branch before
backtracking.
3. Useful for
Deleting Nodes:
- It is useful for deleting nodes from a
tree, as the children are processed before the current node.
4. Expression
Trees:
- Post-order traversal is often used in
expression trees to generate a postfix expression.
Structure of Post-order Tree Traversal:
Algorithm:
Algorithm
postOrderTraversal(node):
Input: Root of the tree or subtree
Output: Post-order traversal of the tree or
subtree
1. If the node is not null:
a. Recursively call postOrderTraversal
with the left child of the node.
b. Recursively call postOrderTraversal
with the right child of the node.
c. Process the node (e.g., print its
value).
Pseudocode:
postOrderTraversal(node):
if node is not null:
postOrderTraversal(node.left)
postOrderTraversal(node.right)
process(node)
Example in C++: cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
void
postOrderTraversal(TreeNode* root) {
if (root != nullptr) {
postOrderTraversal(root->left);
postOrderTraversal(root->right);
cout << root->data <<
" ";
}
}
// Example Usage
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "Post-order Traversal:
";
postOrderTraversal(root);
cout << endl;
return 0;
}
------------------------------
Example in Python: python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def post_order_traversal(root):
if root is not None:
post_order_traversal(root.left)
post_order_traversal(root.right)
print(root.data, end=" ")
# Example Usage
root = TreeNode(1)
root.left =
TreeNode(2)
root.right =
TreeNode(3)
root.left.left =
TreeNode(4)
root.left.right =
TreeNode(5)
print("Post-order
Traversal:", end=" ")
post_order_traversal(root)
print()
----------------------------------------------
Advantages of Post-order Tree Traversal:
1. Deleting Nodes:
- Suitable for deleting nodes from a tree,
as it ensures that child nodes are processed before their parent.
2. Expression
Trees:
- Useful for generating postfix expressions
in expression trees, facilitating easy evaluation.
-----------------------------------------------------------------------
Disadvantages of Post-order Tree Traversal:
1. Not Suitable
for Sorting:
- Like pre-order traversal, post-order
traversal does not produce elements in sorted order, making it less suitable
for sorting tasks.
----------------------------------------------------------------
Application of Post-order Tree Traversal:
1. Deleting Nodes:
- Post-order traversal is useful for
deleting nodes from a tree as it ensures that child nodes are processed before
their parent.
2. Expression
Evaluation:
- Used in expression trees to generate
postfix expressions, which can be directly evaluated.
3. Memory
Management:
- In certain memory management algorithms,
post-order traversal can be applied to release resources associated with nodes.
-------------------------------------------------------
Post-order Tree
Traversal Algorithm:
Algorithm:
Algorithm
postOrderTraversal(node):
Input: Root of the tree or subtree
Output: Post-order traversal of the tree or
subtree
1. If the node is not null:
a. Recursively call postOrderTraversal
with the left child of the node.
b. Recursively call postOrderTraversal
with the right child of the node.
c. Process the node (e.g., print its
value).
Pseudocode:
postOrderTraversal(node):
if node is not null:
postOrderTraversal(node.left)
postOrderTraversal(node.right)
process(node)
-------------------------------------
Example in C++: cpp
#include
<iostream>
using namespace
std;
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val),
left(nullptr), right(nullptr) {}
};
void
postOrderTraversal(TreeNode* root) {
if (root != nullptr) {
postOrderTraversal(root->left);
postOrderTraversal(root->right);
cout << root->data <<
" ";
}
}
// Example Usage
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "Post-order Traversal:
";
postOrderTraversal(root);
cout << endl;
return 0;
}
------------------------------------
Example in Python: python
class TreeNode:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
def
post_order_traversal(root):
if root is not None:
post_order_traversal(root.left)
post_order_traversal(root.right)
print(root.data, end=" ")
# Example Usage
root = TreeNode(1)
root.left =
TreeNode(2)
root.right =
TreeNode(3)
root.left.left =
TreeNode(4)
root.left.right =
TreeNode(5)
print("Post-order
Traversal:", end=" ")
post_order_traversal(root)
print()
-------------------------------------
Difference between inorder, preorder, and postorder tree traversing.
In-order,
Pre-order, and Post-order Tree Traversals are methods to visit and process
nodes in a binary tree in a specific order.
The primary
difference lies in the order in which the nodes are processed.
In-order Tree Traversal:
- Order of
Processing:
- Left subtree, current node, right subtree.
- Application:
- Sorting binary search trees, expression
evaluation, and validation of BST properties.
- Example:
- For a tree with nodes A, B, and C: In-order
traversal would be B, A, C.
Pre-order Tree Traversal:
- Order of
Processing:
- Current node, left subtree, right subtree.
- Application:
- Creating a copy of a tree, and expression
evaluation in certain contexts.
- Example:
- For a tree with nodes A, B, and C:
Pre-order traversal would be A, B, C.
Post-order Tree Traversal:
- Order of
Processing:
- Left subtree, right subtree, current node.
- Application:
- Deleting nodes from a tree, expression
evaluation in certain contexts.
- Example:
- For a tree with nodes A, B, and C:
Post-order traversal would be B, C, A.
Summary of Differences:
1. Order of
Processing:
- In-order: Left subtree, current node,
right subtree.
- Pre-order: Current node, left subtree,
right subtree.
- Post-order: Left subtree, right subtree,
current node.
2. Use Cases:
- In-order: Sorting, and validation of binary
search trees.
- Pre-order: Creating a copy of a tree,
certain expression evaluations.
- Post-order: Deleting nodes from a tree,
certain expression evaluations.
3. Property
Emphasized:
- In-order: Emphasizes the order within a
BST.
- Pre-order: Emphasizes the hierarchy,
starting from the root.
- Post-order: Emphasizes the hierarchy,
ending at the root.
In conclusion, the
choice of traversal depends on the specific requirements of the task at hand.
Each traversal has its unique characteristics and is suitable for different
applications.
------------------------------------------------
B-tree
A B-tree (Balanced
Tree) is a self-balancing search tree data structure that maintains sorted data
and allows searches, insertions, and deletions in logarithmic time.
B-trees are
commonly used in database systems and file systems due to their balanced nature
and efficient disk access patterns.
Features of B-trees:
1. Balanced
Structure:
- B-trees are self-balancing, ensuring that
the depth of the tree remains balanced. This balance allows for efficient
search, insert, and delete operations.
2. Variable Number
of Children:
- Unlike binary trees, B-trees can have more
than two children per node. The number of children is variable and is typically
large.
3. Ordered Data:
- The keys in each node are stored in sorted
order, making B-trees suitable for search operations and range queries.
4. Node Capacity:
- Each internal node in a B-tree has a
variable number of keys within a specified range. The number of keys in a node
is often referred to as the order of the tree.
5. Efficient Disk
Access:
- B-trees are designed to be efficient for
storage systems, with each node typically corresponding to a block or page on
disk. This minimizes disk I/O operations during tree traversal.
6. Guaranteed
Depth:
- Due to their balanced nature, B-trees
guarantee a logarithmic height, ensuring efficient search and retrieval times.
Structure of a B-tree:
A B-tree node
typically consists of the following components:
- Keys:
- Keys are values that determine the order of
the data stored in the node. The keys are stored in sorted order.
- Children
Pointers:
- For internal nodes, there are pointers to
child nodes. The number of pointers corresponds to the number of keys plus one.
- Leaf Nodes:
- Leaf nodes store actual data records. They
do not have child pointers.
- Order:
- The order of a B-tree specifies the minimum
and maximum number of keys a node can have. An order of 't' means each internal
node can have at most 2t - 1 keys and at least t - 1 keys.
Example:-
B-Tree Diagram
Here's a diagram of a B-tree with a minimum degree (t) of 3:
Root (t-1 <= keys <= 2*t-1) / | \ / | \ B1 C2 D3 / \ / \ / \ A1 B2 E1 F2 G1 H3Explanation:
- This is a simple B-tree with the minimum degree (t)
set to 3. This means:
- Each node (except the root) can have a minimum of 2 keys
(t-1) and a maximum of 4 keys (2*t-1).
- Each node (including the root) can have a minimum of 3
children (t) and a maximum of 5 children (2*t).
- Each node contains keys sorted in ascending order.
- All leaf nodes are at the same level (balanced).
- Each child pointer in a non-leaf node points to a
subtree with a key greater than the key preceding it and a key less than
or equal to the key following it.
Example:
- Root: Contains 3 keys (C2, D3, and a key greater than B1 and less than or equal to
E1).
- Node B1: Contains 2 keys (A1 and B2). It points to 3 children
(subtrees with roots A1, B2, and E1).
- Node C2: Contains 1 key. It points to 2 children (subtrees with roots E1 and
F2).
This is just a simplified example. B-trees can have varying degrees and handle much larger
amounts of data efficiently.
Example: Consider a 2-3 B-tree (also known
as a 2-3 tree):
- Each internal
node can have 1 or 2 keys.
- Each internal
node can have 2 or 3 child pointers.
[C]
/
\
[A, B]
[D, E]
/
| | \
[F, G] [I, J] [K]
[L, M]
In this example,
the B-tree has keys {A, B, C, D, E, F, G, I, J, K, L, M}.
Operations on B-trees:
1. Search:
- Efficient search operation with
logarithmic time complexity.
2. Insertion:
- Efficient insertion operation while
maintaining the balance of the tree.
3. Deletion:
- Efficient deletion operation while
maintaining the balance of the tree.
----------------------------------------
Applications:
- File Systems:
- B-trees are widely used in file systems for
efficient indexing and search operations.
- Databases:
- Database systems use B-trees to index large
datasets, enabling efficient retrieval and updates.
- External
Sorting:
- B-trees facilitate efficient external
sorting algorithms, especially when dealing with large datasets that do not fit
entirely in memory.
- Networking:
- B-trees are used in network routers and
switches to optimize routing table lookups.
-----------------------------
Implementing a
B-tree
involves several
operations such as search, insertion, and deletion.
Below is a simple
example of a B-tree in C++ and Python along with the basic operations.
B-tree Algorithm:
A B-tree algorithm
involves the following operations:
1. Search:
- Traverse the tree to find a specific key.
2. Insertion:
- Insert a key into the tree while
maintaining its balance.
3. Deletion:
- Remove a key from the tree while
maintaining its balance.
Example in C++: cpp
#include
<iostream>
#include
<vector>
using namespace
std;
// B-tree node
structure
class BTreeNode {
public:
vector<int> keys;
vector<BTreeNode*> children;
bool isLeaf;
BTreeNode(bool leaf) : isLeaf(leaf) {}
};
class BTree {
private:
BTreeNode* root;
int t; // Minimum degree
// Other private helper functions for
search, insert, delete, and traversal
public:
BTree(int degree) : root(nullptr),
t(degree) {}
// Public interface for search, insert,
delete, and traversal
};
int main() {
BTree btree(3); // Create a B-tree with a
minimum degree of 3
// Perform B-tree operations (search,
insert, delete, etc.)
return 0;
}
--------------------------------------------
Example in Python:python
class BTreeNode:
def __init__(self, leaf):
self.keys = []
self.children = []
self.isLeaf = leaf
class BTree:
def __init__(self, degree):
self.root = None
self.t = degree # Minimum degree
# Other private helper functions for
search, insert, delete, and traversal
# Public interface for search, insert,
delete, and traversal
# Example Usage
btree =
BTree(3) # Create a B-tree with a
minimum degree of 3
# Perform B-tree
operations (search, insert, delete, etc.)
--------------------------------------------
Advantages of B-trees:
1. Balanced
Structure:
- B-trees maintain a balanced structure,
ensuring logarithmic height and efficient search, insert, and delete
operations.
2. Efficient for
Large Datasets:
- B-trees are well-suited for handling large
datasets, especially in external storage systems where nodes correspond to
blocks or pages.
3. Disk I/O
Efficiency:
- The balanced nature of B-trees allows for
efficient disk I/O operations, reducing the number of page accesses during tree
traversal.
4. Versatility in
Degree:
- B-trees can be adjusted to various
degrees, making them versatile and suitable for different application
scenarios.
5. Efficient for
Range Queries:
- B-trees are efficient for range queries,
making them suitable for databases and file systems where range queries are
common.
------------------------------------------
Disadvantages of
B-trees:
1. Complexity in
Implementation:
- The implementation of B-trees can be
complex compared to simpler data structures like binary search trees.
2. Memory
Overhead:
- B-trees can have more significant memory
overhead compared to simpler structures due to the need to store multiple keys
in each node.
------------------------------------------------
Applications of B-trees:
1. Database
Systems:
- B-trees are widely used in database
systems for indexing, allowing efficient search, insert, and delete operations
on large datasets.
2. File Systems:
- File systems often use B-trees for
directory structures and file indexing to optimize search and retrieval.
3. External
Sorting:
- B-trees are used in external sorting
algorithms where large datasets need to be sorted efficiently using disk-based
storage.
4. Networking:
- B-trees are employed in networking devices
like routers and switches for efficient routing table lookups.
5. Geographical
Information Systems (GIS):
- B-trees are used in GIS applications for
indexing spatial data efficiently.
6. Memory
Management:
- B-trees can be utilized in memory
management systems for efficient allocation and deallocation of memory blocks.
7. Transactional
Systems:
- In transactional systems, B-trees are used
to maintain indexes on transactional data for efficient queries.
In summary,
B-trees have significant advantages in terms of balanced structure, efficiency
for large datasets, and versatility in different applications. They are
commonly used in database systems, file systems, networking, and other
scenarios where efficient search and retrieval operations are crucial. However,
their implementation can be more complex compared to simpler data structures,
and they may have some memory overhead.
---------------------------------------------
Height Balance
Tree (AVL Tree)
An AVL tree, named
after its inventors Adelson-Velsky and Landis, is a self-balancing binary
search tree.
It maintains its
balance by ensuring that the heights of the two child subtrees of any node
differ by at most one.
This balance
property helps in achieving efficient search, insert, and delete operations
with logarithmic time complexity.
Features of AVL Tree:
1. Balanced
Structure:
- The defining feature of an AVL tree is its
balance property, ensuring that the heights of the left and right subtrees of
any node differ by at most one.
2. Binary Search
Tree Property:
- AVL trees maintain the binary search tree
(BST) property, where the left subtree of a node contains only nodes with keys
less than the node's key, and the right subtree contains only nodes with keys
greater than the node's key.
3.
Height-Balancing Factor:
- Each node in an AVL tree has a
height-balancing factor, which is the difference between the height of its left
subtree and the height of its right subtree. The balancing factor is limited to
-1, 0, or 1.
4. Rotations:
- AVL trees use rotation operations (single
and double rotations) to maintain balance during insertion and deletion
operations.
---------------------------------
Structure of AVL Tree:
An AVL tree node
typically consists of the following components:
- Key:
- The value that determines the ordering of
nodes in the tree.
- Pointers to Left
and Right Children:
- Pointers to the left and right children
nodes, which are the roots of the left and right subtrees.
- Height:
- The height of the node, defined as the
length of the longest path from the node to a leaf node.
- Balance Factor:
- The balance factor, which is the difference
between the height of the left subtree and the height of the right subtree. It
is limited to -1, 0, or 1 to maintain balance.
---------------------------------------
Example of AVL Tree:
Consider the
following AVL tree:
30
/
\
20
40
/
\ / \
10
25 35 50
In this example,
the AVL tree maintains its balance at every level, ensuring that the heights of
left and right subtrees of each node differ by at most one.
Example:-
Here's a diagram of an AVL Tree:
20 / \ 10 30 / \ / \ 5 15 25 40 / \ / \ 3 8 35 45 Balance Factors: - 20: 0 (balanced) - 10: 1 (balanced) - 30: -1 (balanced) - 5: 0 (balanced) - 15: 0 (balanced) - 25: 0 (balanced) - 40: 1 (balanced) - 3: 0 (balanced) - 8: 0 (balanced) - 35: 0 (balanced) - 45: 0 (balanced)Explanation:
·
This AVL Tree represents the data: 20, 10, 30, 5, 15, 25, 40, 3, 8, 35, 45.
·
Each node contains a value and its
balance factor.
·
The balance factor is calculated by
subtracting the height of the right subtree from the height of the left subtree.
·
An AVL Tree is considered balanced
if the balance factor of each node is either -1, 0, or 1.
·
In this example, all nodes are balanced.
Additional points:
·
AVL Trees require additional
operations compared to standard Binary Search Trees to maintain their balance
properly after insertion or deletion.
·
Despite the extra overhead, AVL Trees guarantee a worst-case time complexity of O(log
n) for search, insertion, and deletion operations, making them efficient for data
structures requiring frequent modifications.
Operations on AVL Tree:
1. Search:
- Efficient search operation with
logarithmic time complexity, similar to other binary search trees.
2. Insertion:
- Insertion operations involve performing
rotations to maintain the AVL tree's balance.
3. Deletion:
- Deletion operations involve performing
rotations to maintain the AVL tree's balance.
Rotations in AVL Tree:
1. Left Rotation:
- Restores balance when the right subtree is
taller.
2. Right Rotation:
- Restores balance when the left subtree is
taller.
3. Left-Right
Rotation:
- Combines a left rotation followed by a
right rotation to restore balance.
4. Right-Left
Rotation:
- Combines a right rotation followed by a
left rotation to restore balance.
Summary:
AVL trees are a
type of self-balancing binary search tree that ensures logarithmic time
complexity for search, insert, and delete operations. Their balance is
maintained through rotation operations. The AVL tree's structure and balancing
properties make it suitable for scenarios where the dataset is subject to
frequent modifications and needs to remain balanced for efficient operations.
----------------------------------------------------------------------
AVL tree
implementation in C++ and Python
AVL Tree Algorithm:
1. Node Structure:
- Define a structure for the AVL tree node,
including key, pointers to left and right children, height, and balance factor.
2. Rotation
Functions:
- Implement rotation functions for left
rotation, right rotation, left-right rotation, and right-left rotation.
3. Insertion
Operation:
- Implement the insertion operation,
ensuring that the AVL tree remains balanced after the insertion.
4. Search
Operation:
- Implement the search operation to find a
specific key in the AVL tree.
5. In-order
Traversal:
- Implement in-order traversal to display
the elements in sorted order.
Example in C++:cpp
#include
<iostream>
#include
<algorithm>
using namespace
std;
struct AVLNode {
int key;
AVLNode* left;
AVLNode* right;
int height;
};
class AVLTree {
public:
AVLNode* root;
AVLTree() : root(nullptr) {}
// Utility function to get height of a node
int getHeight(AVLNode* node) {
return (node == nullptr) ? 0 :
node->height;
}
// Utility function to calculate balance
factor of a node
int getBalanceFactor(AVLNode* node) {
return (node == nullptr) ? 0 :
getHeight(node->left) - getHeight(node->right);
}
// Utility function to update height of a
node
void updateHeight(AVLNode* node) {
if (node != nullptr)
node->height = 1 +
max(getHeight(node->left), getHeight(node->right));
}
// Rotation functions
AVLNode* leftRotate(AVLNode* y) {
AVLNode* x = y->right;
AVLNode* T2 = x->left;
x->left = y;
y->right = T2;
updateHeight(y);
updateHeight(x);
return x;
}
AVLNode* rightRotate(AVLNode* x) {
AVLNode* y = x->left;
AVLNode* T2 = y->right;
y->right = x;
x->left = T2;
updateHeight(x);
updateHeight(y);
return y;
}
AVLNode* insert(AVLNode* node, int key) {
// Perform standard BST insertion
if (node == nullptr)
return new AVLNode{key, nullptr,
nullptr, 1};
if (key < node->key)
node->left =
insert(node->left, key);
else if (key > node->key)
node->right =
insert(node->right, key);
else
return node; // Duplicate keys are
not allowed
// Update height of the current node
updateHeight(node);
// Get the balance factor to check if
rotation is needed
int balance = getBalanceFactor(node);
// Perform rotations if needed
// Left Heavy
if (balance > 1) {
if (key < node->left->key)
// Left-Left
return rightRotate(node);
else // Left-Right
{
node->left =
leftRotate(node->left);
return rightRotate(node);
}
}
// Right Heavy
if (balance < -1) {
if (key >
node->right->key) // Right-Right
return leftRotate(node);
else // Right-Left
{
node->right =
rightRotate(node->right);
return leftRotate(node);
}
}
return node;
}
// Utility function for in-order traversal
void inOrderTraversal(AVLNode* root) {
if (root != nullptr) {
inOrderTraversal(root->left);
cout << root->key <<
" ";
inOrderTraversal(root->right);
}
}
};
int main() {
AVLTree avlTree;
// Inserting keys
avlTree.root = avlTree.insert(avlTree.root,
10);
avlTree.root = avlTree.insert(avlTree.root,
20);
avlTree.root = avlTree.insert(avlTree.root,
30);
// In-order traversal
cout << "In-order Traversal:
";
avlTree.inOrderTraversal(avlTree.root);
cout << endl;
return 0;
}
---------------------------------------
Example in Python:python
class AVLNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree:
def __init__(self):
self.root = None
def get_height(self, node):
return node.height if node else 0
def update_height(self, node):
if node:
node.height = 1 +
max(self.get_height(node.left), self.get_height(node.right))
def get_balance_factor(self, node):
return self.get_height(node.left) -
self.get_height(node.right) if node else 0
def left_rotate(self, y):
x = y.right
T2 = x.left
x.left = y
y.right = T2
self.update_height(y)
self.update_height(x)
return x
def right_rotate(self, x):
y = x.left
T2 = y.right
y.right = x
x.left = T2
self.update_height(x)
self.update_height(y)
return y
def insert(self, root, key):
if not root:
return AVLNode(key)
if key < root.key:
root.left = self.insert(root.left,
key)
elif key > root.key:
root.right =
self.insert(root.right, key)
else:
return root # Duplicate keys are not allowed
# Update height of the current node
self.update_height(root)
# Get the balance factor to check if
rotation is needed
balance = self.get_balance_factor(root)
# Perform rotations if needed
# Left Heavy
if balance > 1:
if key < root.left.key: # Left-Left
return self.right_rotate(root)
else: # Left-Right
root.left =
self.left_rotate(root.left)
return self.right_rotate(root)
# Right Heavy
if balance < -1:
if key > root.right.key: # Right-Right
return self.left_rotate(root)
else: # Right-Left
root.right =
self.right_rotate(root.right)
return self.left_rotate(root)
return root
# Utility function for in-order traversal
def in_order_traversal(self, root):
if root:
self.in_order_traversal(root.left)
print(root.key, end=" ")
self.in_order_traversal(root.right)
if __name__ ==
"__main__":
avl_tree = AVLTree()
# Inserting keys
avl_tree.root =
avl_tree.insert(avl_tree.root, 10)
avl
_tree.root =
avl_tree.insert(avl_tree.root, 20)
avl_tree.root =
avl_tree.insert(avl_tree.root, 30)
# In-order traversal
print("In-order Traversal:",
end=" ")
avl_tree.in_order_traversal(avl_tree.root)
print()
-----------------------------------
Advantages of AVL
Trees:
1. Balanced
Structure:
- AVL trees maintain a balanced structure,
ensuring that the height difference between the left and right subtrees of any
node is at most one. This balance guarantees efficient search, insert, and
delete operations with logarithmic time complexity.
2. Efficient
Operations:
- Search, insert, and delete operations on
AVL trees have logarithmic time complexity, making them efficient for dynamic
datasets.
3. Predictable
Performance:
- AVL trees provide predictable performance
in terms of time complexity, as their balance ensures that the height remains
logarithmic.
4. Versatile:
- AVL trees are versatile and can be used in
various applications where dynamic datasets require efficient search and
modification operations.
---------------------------------------
Disadvantages of
AVL Trees:
1. Overhead of
Balancing:
- The balancing mechanism in AVL trees adds
extra overhead to each operation, making them slightly less efficient than
simpler data structures, especially for datasets that do not change frequently.
2. Complexity in
Implementation:
- The implementation of AVL trees involves
complex rotations to maintain balance, making the code more intricate compared
to simpler tree structures.
------------------------------------------
Applications of AVL Trees:
1. Database
Systems:
- AVL trees are widely used in database
systems for indexing, ensuring efficient search and retrieval of records.
2. Compiler
Design:
- In compiler design, AVL trees are used in
symbol tables for efficient lookup of identifiers.
3. File Systems:
- AVL trees are utilized in file systems for
maintaining directory structures and efficient lookup of file information.
4. Networking:
- In networking, AVL trees can be employed
for routing tables to optimize the lookup of network addresses.
5. Caches:
- AVL trees can be used in caches for
efficient management of cached items.
6. Transactional
Systems:
- In transactional systems, AVL trees can be
used for maintaining indexes on transactional data.
7. Memory
Management:
- AVL trees can be applied in memory
management systems for efficient allocation and deallocation of memory blocks.
8. Geographical
Information Systems (GIS):
- AVL trees are used in GIS applications for
indexing and querying spatial data.
Summary
AVL trees are
advantageous for their balanced structure, providing efficient search and
modification operations.
They find
applications in various domains where efficient handling of dynamic datasets is
crucial, although the complexity of balancing operations should be considered
in certain scenarios.
=====================================================================







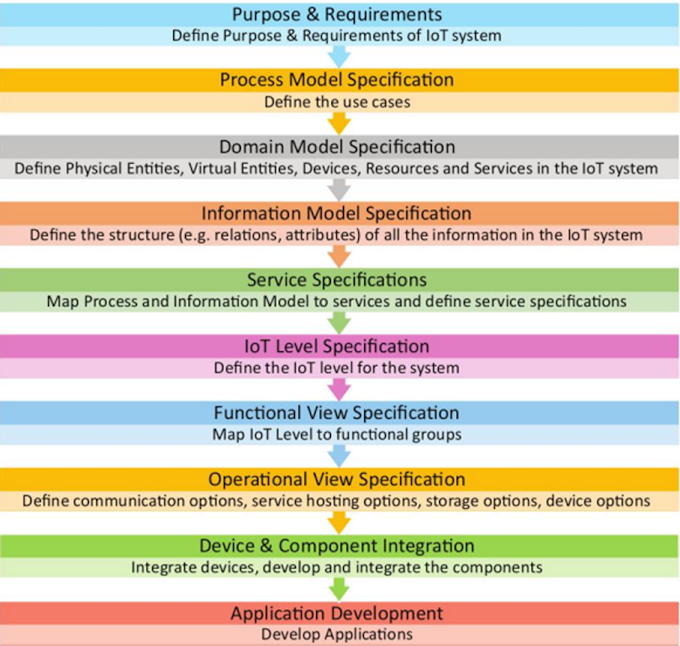
0 Comments